Elliptic Curve Key Generation Algorithm
Author Nick Sullivan worked for six years at Apple on many of its most important cryptography efforts before recently joining CloudFlare, where he is a systems engineer. He has a degree in mathematics from the University of Waterloo and a Masters in computer science with a concentration in cryptography from the University of Calgary. This post was originally written for the CloudFlare blog and has been lightly edited to appear on Ars.
- Elliptic Curve Key Generation
- Elliptic Curve Cryptography Example
- Elliptic Curve Key Generation Algorithm Examples
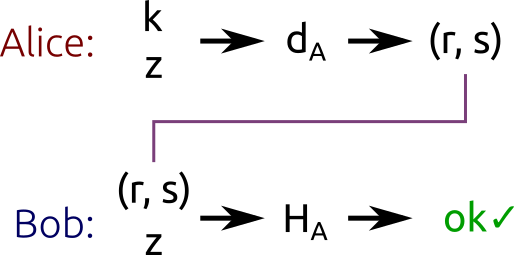
Readers are reminded that elliptic curve cryptography is a set of algorithms for encrypting and decrypting data and exchanging cryptographic keys. Dual_EC_DRBG, the cryptographic standard suspected of containing a backdoor engineered by the National Security Agency, is a function that uses elliptic curve mathematics to generate a series of random-looking numbers from a seed. This primer comes two months after internationally recognized cryptographers called on peers around the world to adopt ECC to avert a possible 'cryptopocalypse.'
Elliptic curve cryptography (ECC) is one of the most powerful but least understood types of cryptography in wide use today. An increasing number of websites make extensive use of ECC to secure everything from customers' HTTPS connections to how they pass data between data centers. Fundamentally, it's important for end users to understand the technology behind any security system in order to trust it. To that end, we looked around to find a good, relatively easy-to-understand primer on ECC in order to share with our users. Finding none, we decided to write one ourselves. That is what follows.
Be warned: this is a complicated subject, and it's not possible to boil it down to a pithy blog post. In other words, settle in for a bit of an epic because there's a lot to cover. If you just want the gist, here's the TL;DR version: ECC is the next generation of public key cryptography, and based on currently understood mathematics, it provides a significantly more secure foundation than first-generation public key cryptography systems like RSA. If you're worried about ensuring the highest level of security while maintaining performance, ECC makes sense to adopt. If you're interested in the details, read on.
The dawn of public key cryptography
The history of cryptography can be split into two eras: the classical era and the modern era. The turning point between the two occurred in 1977, when both the RSA algorithm and the Diffie-Hellman key exchange algorithm were introduced. These new algorithms were revolutionary because they represented the first viable cryptographic schemes where security was based on the theory of numbers; it was the first to enable secure communication between two parties without a shared secret. Cryptography went from being about securely transporting secret codebooks around the world to being able to have provably secure communication between any two parties without worrying about someone listening in on the key exchange.
Provides a Cryptography Next Generation (CNG) implementation of the Elliptic Curve Diffie-Hellman (ECDH) algorithm. This class is used to perform cryptographic operations. ECDiffieHellmanCng Class (System.Security.Cryptography) Microsoft Docs. May 22, 2015 Elliptical Curve Cryptography. Elliptic Curve Cryptography (ECC) is a public key cryptography. In public key cryptography each user or the device taking part in the communication generally have a pair of keys, a public key and a private key, and a set of operations associated with the keys.
Modern cryptography is founded on the idea that the key that you use to encrypt your data can be made public while the key that is used to decrypt your data can be kept private. As such, these systems are known as public key cryptographic systems. The first, and still most widely used of these systems, is known as RSA—named after the initials of the three men who first publicly described the algorithm: Ron Rivest, Adi Shamir, and Leonard Adleman.
What you need for a public key cryptographic system to work is a set of algorithms that is easy to process in one direction but difficult to undo. In the case of RSA, the easy algorithm multiplies two prime numbers. If multiplication is the easy algorithm, its difficult pair algorithm is factoring the product of the multiplication into its two component primes. Algorithms that have this characteristic—easy in one direction, hard the other—are known as trapdoor functions. Finding a good trapdoor function is critical to making a secure public key cryptographic system. Simplistically, the bigger the spread between the difficulty of going one direction in a trapdoor function and going the other, the more secure a cryptographic system based on it will be.
Git windows generate ssh key. Ssh-keygen -t rsa -b 4096 -C 'your github's email' # Creates a new ssh key # Generating public/private rsa key pair. This will generate a key for you.You have to copy that and insert into your Github's account (just one time). Steps how to do It. Generating Your SSH Public Key. Many Git servers authenticate using SSH public keys. In order to provide a public key, each user in your system must generate one if they don’t already have one. This process is similar across all operating systems. First, you should check to make sure you don’t already have a key.
A toy RSA algorithm
The RSA algorithm is the most popular and best understood public key cryptography system. Its security relies on the fact that factoring is slow and multiplication is fast. What follows is a quick walk-through of what a small RSA system looks like and how it works.
In general, a public key encryption system has two components, a public key and a private key. Encryption works by taking a message and applying a mathematical operation to it to get a random-looking number. Decryption takes the random looking number and applies a different operation to get back to the original number. Encryption with the public key can only be undone by decrypting with the private key.

Computers don't do well with arbitrarily large numbers. We can make sure that the numbers we are dealing with do not get too large by choosing a maximum number and only dealing with numbers less than the maximum. We can treat the numbers like the numbers on an analog clock. Any calculation that results in a number larger than the maximum gets wrapped around to a number in the valid range.
In RSA, this maximum value (call it max) is obtained by multiplying two random prime numbers. The public and private keys are two specially chosen numbers that are greater than zero and less than the maximum value (call them pub and priv). To encrypt a number, you multiply it by itself pub times, making sure to wrap around when you hit the maximum. To decrypt a message, you multiply it by itself priv times, and you get back to the original number. It sounds surprising, but it actually works. This property was a big breakthrough when it was discovered.
To create an RSA key pair, first randomly pick the two prime numbers to obtain the maximum (max). Then pick a number to be the public key pub. As long as you know the two prime numbers, you can compute a corresponding private key priv from this public key. This is how factoring relates to breaking RSA—factoring the maximum number into its component primes allows you to compute someone's private key from the public key and decrypt their private messages.
Let's make this more concrete with an example. Take the prime numbers 13 and 7. Their product gives us our maximum value of 91. Let's take our public encryption key to be the number 5. Then using the fact that we know 7 and 13 are the factors of 91 and applying an algorithm called the Extended Euclidean Algorithm, we get that the private key is the number 29.
These parameters (max: 91, pub: 5, priv: 29) define a fully functional RSA system. You can take a number and multiply it by itself 5 times to encrypt it, then take that number and multiply it by itself 29 times and you get the original number back.
Let's use these values to encrypt the message 'CLOUD'.
In order to represent a message mathematically, we have to turn the letters into numbers. A common representation of the Latin alphabet is UTF-8. Each character corresponds to a number.
Under this encoding, CLOUD is 67, 76, 79, 85, 68. Each of these digits is smaller than our maximum of 91, so we can encrypt them individually. Let's start with the first letter.
We have to multiply it by itself five times to get the encrypted value.
67×67 = 4489 = 30 *
*Since 4489 is larger than max, we have to wrap it around. We do that by dividing by 91 and taking the remainder.
4489 = 91×49 + 30
30×67 = 2010 = 8
8×67 = 536 = 81
81×67 = 5427 = 58
This means the encrypted version of 67 (or C) is 58.
Repeating the process for each of the letters, we get that the encrypted message CLOUD becomes:
58, 20, 53, 50, 87
To decrypt this scrambled message, we take each number and multiply it by itself 29 times:
58×58 = 3364 = 88 (Remember, we wrap around when the number is greater than max.)
88×58 = 5104 = 8
…
9×58 = 522 = 67
Voila, we're back to 67. This works with the rest of the digits, resulting in the original message.
The takeaway is that you can take a number, multiply it by itself a number of times to get a random-looking number, and then multiply that number by itself a secret number of times to get back to the original number.
The ECC (Elliptic Curve Cryptography) algorithm was originally independently suggested by Neal Koblitz (University of Washington), and Victor S. Miller (IBM) in 1985. Although the ECC algorithm was proposed for cryptography in 1985, it has had a slow start and it took nearly twenty years, until 2004 and 2005, for the scheme to gain wide acceptance. ECC (Elliptic Curve Cryptography) is a relatively new algorithm that creates encryption keys based on using points on a curve to define the public and private keys.
Key Benefits of ECC
ECC key is very helpful for the current generation as more people are moving to the Smartphone. As the utilization of Smartphone extends to grow, there is an emerging need for a more flexible encryption for business to meet with increasing security requirements.
Stronger Keys
Elliptic Curve Key Generation
ECC stands for Elliptic Curve Cryptography is the latest encryption method offers stronger security. If we compare to the RSA and DSA algorithms, then 256-bit ECC is equal to 3072-bit RSA key. The reason behind keeping short key is the use of less computational power, fast and secure connection, ideal for Smartphone and tablet too.
The US government and the National Security Agency have certified ECC encryption method. The mathematical problem of the ECC algorithm, It is harder to break for hackers compare to RSA and DSA, which means the ECC algorithm ensures web site and infrastructure safety than traditional methods in a more secure manner.
Shorter Key Size
The elliptic curve cryptography (ECC) certificates allow key size to remain small while providing a higher level of security. ECC certificates key creation method is entirely different from previous algorithms, while relying on the use of a public key for encryption and a private key for decryption. By starting small and with a slow growth potential, ECC has longer potential lifespan. Elliptic curves are likely to be the next generation of cryptographic algorithms, and we are seeing the beginning of their use now.
| Minimum size (bits) of Public Keys | Key Size Ratio | |||
| Security (bits) | DSA / RSA | ECC | ECC to RSA / DSA | Valid |
| 80 | 1024 | 160-223 | 1:6 | Until 2010 |
| 112 | 2048 | 224-255 | 1:9 | Until 2030 |
| 128 | 3072 | 256-383 | 1:12 | Beyond 2031 |
| 192 | 7680 | 384-511 | 1:20 | |
| 256 | 15360 | 512+ | 1:30 | |
If we examine the above table, there is a considerable growth in DSA and RSA key than ECC key size. A longer key requires more space, more bandwidth, and additional processor power. Even, it will take a time to generate a key, encrypt data, and decrypt the data.
Why Elliptic Curve Cryptography is Required?
Encryption experts are pressed to find ever more effective methods, measured in security and performance, because the threats presented by hackers are ever greater – partly because the hackers themselves become more sophisticated in their attacks, and also because the fallout from an attack gets ever more dangerous as our use of data grows. It creates an urgency of new algorithms with a goal to provide a higher level of security by having keys that are more difficult to break, while offering better performance across the network and while working with large data sets.
Several factors are contributing to its increasing popularity. First of all, the security of 1024-bit encryption is degrading, due to faster computing and a better understanding and analysis of encryption methods. While brute force is still unlikely to crack 1024-bit encryption, other approaches, including highly intensive parallel computing in distributed computing arrays, are resulting in more sophisticated attacks. These attacks have reduced the effectiveness of this level of security. Even 2048-bit encryption is estimated by the RSA Security to be effective only until 2030.
- Web standards: Business owner has to mull over web server standards. Many web servers running on a single domain name can handle RSA, DSA, and ECC configuration. On the other side, few web servers do not have the ability to handle multiple algorithms and can utilize a single certificate on a single web server.
- Authentication speed: RSA, DSA, and ECC have diverse velocity for verification and authentication. RSA is a rapid algorithm in terms of client authentication while ECC is faster in terms of server authentication. Signature verification is rapidly in case of RSA key comparing to ECC key. There are transaction types, the processing power of the device; storage capacity, bandwidth, and consumption of power also influence the algorithm selection.
- Customer’s identity: Many government entities have started to accept DSA and ECC. They required for government subcontracts, government branches for their internal exchange of communication.
Elliptic Curve Cryptography Example
The number of connections plays a vital role in selecting algorithm standard. ECC can handle more connections at the same time compare to RSA algorithm. An Organization has to maintain the balance between security, user experience, and IT infrastructure cost involved in network process.
Get ECC Enabled SSL
To give true benefits of enhanced security, certificate authorities have started to embed ECC and DSA algorithm in their SSL certificates. Comodo has started to provide the ECC SSL certificates with keeping the emerging demand of Smartphone and other Compaq devices.
| If you are looking for ECC SSL certificate at affordable price then buy Comodo SSL certificate from us and get enhanced level security to your website. |
Elliptic Curve Key Generation Algorithm Examples
We are authorized reseller of Comodo that make your purchase worthful. You will get premium-class security with Comodo SSL certificates that will establish your brand reputation over the web.